算数の苦手の克服「文章題」「図形」「数の性質」
中学受験を成功させていく上で、もっとも重要なことは
「算数を得意科目にする」ということです。
たとえ得意にならなくても、
お子さんが算数に対する苦手の意識を持たないことが肝心です。
実際の入試の結果でも、算数の差が合否を分けています。
下の表を見てください。
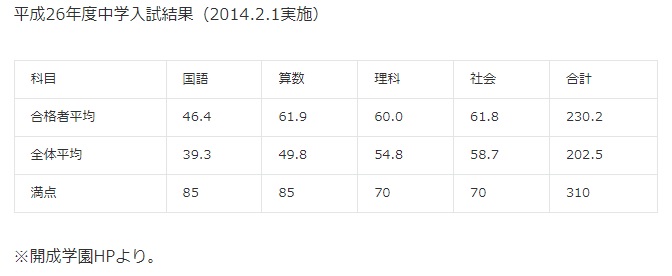
上の表から分かるように、
(合格者平均)-(全体平均)で最も大きな数字は「算数」です。
12.1点も差があります。社会はわずか3.1点です。
合格者は算数でかせいで合格しているのが良く分かりますね。
受験の合否は算数が握っているのです。
もし現在、お子さんが「算数が苦手」だとか、
「算数の点数が伸びない」という状態でも決してあわてないでください。
まずは次のことを理解してください。
苦手だとか得点ができない。
…といっても、算数のどの分野がそのようになっているのかを、
まずチェックすることから始めましょう。
受験算数には、計算問題以外に次の3つの分野に分かれます。
◆『文章題』◆
「速さ」や「割合」の単元と、色んな特殊算です。
旅人算・流水算・時計算・通過算・速さと比・相当算・売買算
食塩水の混ぜ合わせ・つるかめ算・植木算・仕事算…など
◆『図形』◆
「平面図形」と「立体図形」に分れます。
① 平面図形…面積・角度・平面図形と比…など
② 立体図形…体積・表面積・展開図・水位とグラフ…など
◆『数の性質』◆
「公倍数・公約数」「規則性」「場合の数」…など
まずは、
どこでつまづいているのかを認識することが初めの一歩なのです。
おさえるべき算数の基礎力とは?
「算数は基礎力がすべてである」…という言葉をよく聞きますね。
まったくその通りなのです。
そして、基礎の積み重ねの学問なのです。
6年生になって急に成績の伸びが止まった。
新しいテキストになって急に理解できなくなった。
…とかの悩みを持っていらっしゃる方も多いと思います。

特に顕著なのが「算数」です。
6年生だけではありませんね。
4年生から5年生、3年生から4年生へあがる時にも、
当てはまる場合があるでしょう。
物事に結果があるということは、必ず原因が存在します。
では、その原因とは何でしょう?
●算数は積み重ねの教科である。
…ということを再確認しましょうね。
理科や社会は違います。
例えば社会で、歴史がまったくダメでも地理が好きなら得点できますね。
それに対して、算数はどこかが定着していないと、
そこから先の理解は出来ないんです。
図を書いて説明します。
積み木をイメージしてください。
■■■■■■■■■■■■ ← 4年生の基礎力
…の上に、5年生で学ぶことが乗ってきます。
■■■■■■■■■■■■ ← 5年生で学ぶこと
■■■■■■■■■■■■ ← 4年生の基礎力
ここで、4年生の基礎力が、
■■■■■■■ これしかなかったら、
5年生で学ぶことを上乗せしても、
■■■■■■■■■■■■
■■■■■■■↓↓↓↓↓ 落っこちる。
で、結局
■■■■■■■
■■■■■■■ これだけの基礎力しか得ていない。
…という状況になってきますよね。
つまり、落っこちた分が理解できない箇所となっているんです。
だから、今どこかでつまづいているなら、
過去のどこかで、定着できていない所があります。
一番分かりやすい例で言います。
「比」をしっかり理解していないと、「速さと比」は理解不可能です。
「旅人算」の基本2パターン(出会う・追い越す)が定着していなければ、
「通過算・流水算」は理解不可能です。
ですから、何かの単元が良く理解できないとか、
何度やっても得点に結びつかないという状況なら、
一度立ち止まって少し前の基礎が理解できているかどうかをチェックする必要があります。
算数の成績を上げるための勉強法とは?
上でみてきましたように、各学年の基礎力が定着していないと、
次の学年の学習内容がしっかりと理解できないことになってきます。
ここで「定着」という状態も重要です。
定着は「理解した」ではないのです。
お子さんに「ここまでわかりましたか?」と聞いて、
「はーい」と答えることとは違うのです。
定着の状態の説明をするのは難しいのですが、
例えばこんな感じです。
「理解した」「わかった」
→ 地図を見ながら目的地まで行ける(隣町へのお使いのような感じ)
それに対して「定着」
→ 朝起きて寝ぼけていても目的地まで行ける(毎朝、学校へ行く感じ)
伝わったでしょうか?
ここまではご理解いただけたでしょうか?
もう少し例え話をあげると、
分数の通分のとき、2/3 + 2/5 = のような計算のとき、
まだ計算方法を理解して間もない人は、
「ええと、3と5の最小公倍数は、、、、15か、分母に書いて」
…という感じですね。
定着したというレベルは、
この計算式を見た瞬間に分母に15を書いている状態です。
算数の応用問題は線分図のマスターから
さて、結論になります。
私が昔から個別指導塾や家庭教師をしていて気づいたことがあります。
それは、
●問題を読んで、子供たちは「絵」を書こうとしない。
逆に、算数が良くできるお子さんは、問題を読むと(読みながら)絵や図を書いていきます。
どうして、問題を読んで絵や図を書こうとしないのか?
→ 書き方が分からない。書くことの重要性が分からない。
からなのです。
そして、絶対に書かなくてはいけないものが【線分図】という図です。
このような図ですね。

お子さんは、ノートにこのような図をしっかり書いていますか?
一度、ノートをチェックしてあげてくださいね。
問題を読んですぐに、この線分図を書く習慣ができると、
「年令算」をいつまでも、二人の年齢を書き出していく…ことはしなくなります。
【参考動画】年齢算・倍数算のコツ
まとめ
以上、ご説明してきましたが、
算数が苦手だ!うちの子は私に似て文系だから、
もう算数はあきらめたんです。
…という弱音を吐く必要はありません。
算数の基礎力をしっかり定着させておくと、
「算数は苦手です!」という状況には決してならないのです。
そのためには、
できることなら低学年(4年生ぐらい)から
【線分図】を書くことが習慣になっているのがベストですね。
線分図=絵を描いて考える習慣です。
たとえば、以下の4つの問題の図(線分図)が、
スラスラ書ける状態なら大丈夫です。プリントアウトして試してみてください。
PDFファイルをご用意しましたのでダウンロードしてお使いください。
【レベル1】
パパは、念願のマイホームを買う事にしました。
家族みんな大騒ぎ…です。
郊外なので、少し安く、3378万円なのだ!!
パパとママの貯金から、はらうことになりました。
パパは、ママより1178万円多くはらいます。
線分図を書きましょう。
パパとママは、それぞれいくらはらうのでしょう。
【レベル2】
巨人対ロサンゼルス・エンジェルス戦が行われました。
大谷翔平のいるエンジェルス打線はスゴイ!!
大谷の3本のホームランがとびだしました。
エンジェルスの取った得点は、巨人の取った得点の3倍より、
1点少なく、両チームの得点合計は15点でした。
線分図を書きましょう。
エンジェルスは何点、巨人は何点取りましたか?
【レベル3】
あるお店で、「鬼滅の刃」と「ドラエもん」のぬいぐるみを売り出しました。
売上は「鬼滅の刃」の方が、良く売れ、売上金は、「ドラエもん」
の3倍でした。そして売上金の差は、12万円でした。
僕は、「ドラエもん」の方が好きなのに、人は十人十色
だなあ…と思いました。
線分図を書きましょう。
それぞれのぬいぐるみの、売上金を求めましょう。
【レベル4】
今日は私の家にお友達が集まりました。
実はパパは、お菓子の会社に行っているので、
おやつは、いつも「チョコボール」です。
そのチョコボールを配って行きます。
1人8個ずつ配ると2個不足し、
泣きそうになっている子がいます。
1人6個ずつ配ると12個余り、チョコ好きのマイちゃんが歌を
うたいはじめました。
お友達は何人いるでしょう?
またチョコボールは何個あったでしょう?
線分図を書きましょう。
———————————————————–
いかがです?基礎レベルは、クリアしていますか?
ここでは、【レベル4】の差集め算(過不足算)の
線分図が少し難しいかな?
【ミスター・ツカムのワクワク教材】では、
以下のように、お子さんにイメージしやすいようにテキストを作成しています。
そして、「年令算」「倍数算」「和差算」などの問題別に
練習する問題をそろえています。
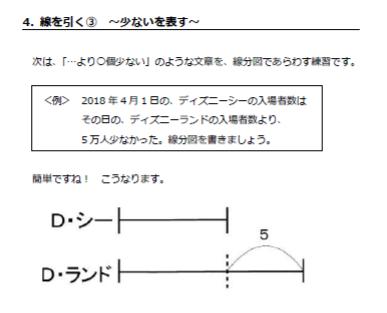
まず、このテキストを使って、何度も何度も【線分図】を書く練習をしてください。
そして、【線分図】が定着できたなら、
そこからは算数の成績も上がってくることと思います。
ミスター・ツカムのワクワク教材お問い合わせ → コチラ(無料)
その他、あわせて読みたいお勧め記事
中学受験 算数の応用問題ができない理由とは?





